Introduction
RL Circuit consists of resistors and Inductors. Depending on the configuration, RL circuit can be applied in various fields. For example, RL circuit can be used as a relay circuit.
Magnitude of Inductance
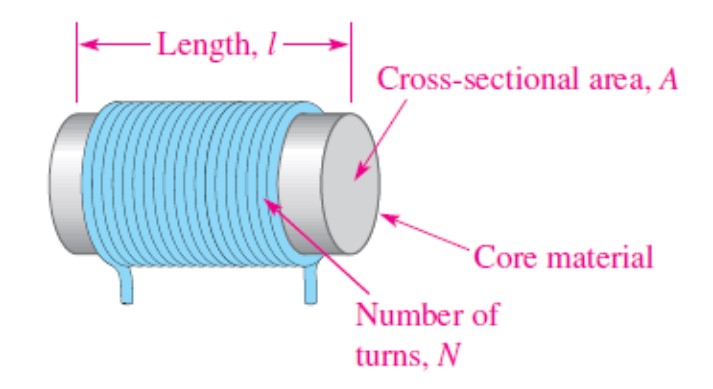
Voltage
Faraday’s Law
The amount of voltage induced in a coil is directly proportional to the rate of change of the magnetic field with respect to the coil.
The electromotive force around a closed path is equal to the negative of the time rate of change of the magnetic flux enclosed by the path.
With Faraday’s Law, we can find the equation for the amount of induced voltage.
\[{\vert}V_{ind}{\vert} = N{d\phi \over dt}\]Lenz’s Law
When the current through a coil changes, an induced voltage is created as a result of the changing electromagnetic field and the polarity of the induced voltage is such that it always opposes the change in current.
With Lenz’s Law, we can find the direction of the induced voltage.
\[V_{ind} = -N{d\phi \over dt}\]Step Response
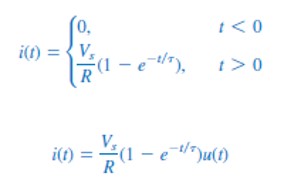
Practical Issues
Winding Resistance
When a coil is made of a certain material, for example, insulated copper wire, that wire has a certain resistance per unit of length. In many applications, the winding resistance may be small enough to be ignored and the coil can be considered an ideal inductor. In other cases, the resistance must be considered.
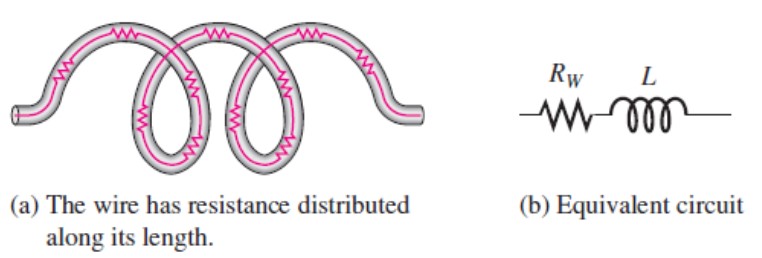
Q Factor
This resistance dissipates some of the reactive energy. The quality factor (or Q) of an inductor is the ratio of its inductive reactance to its resistance at a given frequency, and is a measure of its efficiency. The higher the Q factor of the inductor, the closer it approaches the behavior of an ideal inductor.
\(Q = {wL \over R}\)
Winding Capacitance
When two conductors are placed side by side, there is always some capacitance between them. In many applications, this winding capacitance is very small and has no significant effect. In other cases, particularly at high frequencies, it may become quite important.
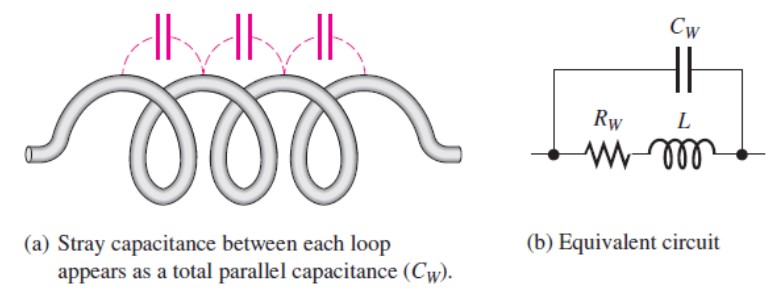
Saturation
Types of Inductors
Air-core Inductor
The term air core coil describes an inductor that does not use a magnetic core made of a ferromagnetic material. The term refers to coils wound on plastic, ceramic, or other nonmagnetic forms, as well as those that have only air inside the windings. Air core coils have lower inductance than ferromagnetic core coils, but are often used at high frequencies because they are free from energy losses called core losses that occur in ferromagnetic cores, which increase with frequency. A side effect that can occur in air core coils in which the winding is not rigidly supported on a form is ‘microphony’: mechanical vibration of the windings can cause variations in the inductance.

Ferromagnetic-core inductor
Ferromagnetic-core or iron-core inductors use a magnetic core made of a ferromagnetic or ferrimagnetic material such as iron or ferrite to increase the inductance. A magnetic core can increase the inductance of a coil by a factor of several thousand, by increasing the magnetic field due to its higher magnetic permeability. However the magnetic properties of the core material cause several side effects which alter the behavior of the inductor.

Side Effects - Core losses
A time-varying current in a ferromagnetic inductor, which causes a time-varying magnetic field in its core, causes energy losses in the core material that are dissipated as heat, due to Eddy currents, Hysteresis.
Eddy currents
From Faraday’s law of induction, the changing magnetic field can induce circulating loops of electric current in the conductive metal core. The energy in these currents is dissipated as heat in the resistance of the core material. The amount of energy lost increases with the area inside the loop of current.
Under certain assumptions (uniform material, uniform magnetic field, no skin effect, etc.) the power lost due to eddy currents per unit mass for a thin sheet or wire can be calculated from the following equation.
\[P_{e} = { { {\phi}^{2}{B_{p}}^{2}d^{2}f^{2} } \over {6k{\rho}D} }\]P is the power lost per unit mass (W/kg),
\(B_{p}\) is the peak magnetic field (T),
d is the thickness of the sheet or diameter of the wire (m),
f is the frequency (Hz),
k is a constant equal to 1 for a thin sheet and 2 for a thin wire,
ρ is the resistivity of the material (Ω m), and
D is the density of the material (kg/m3).
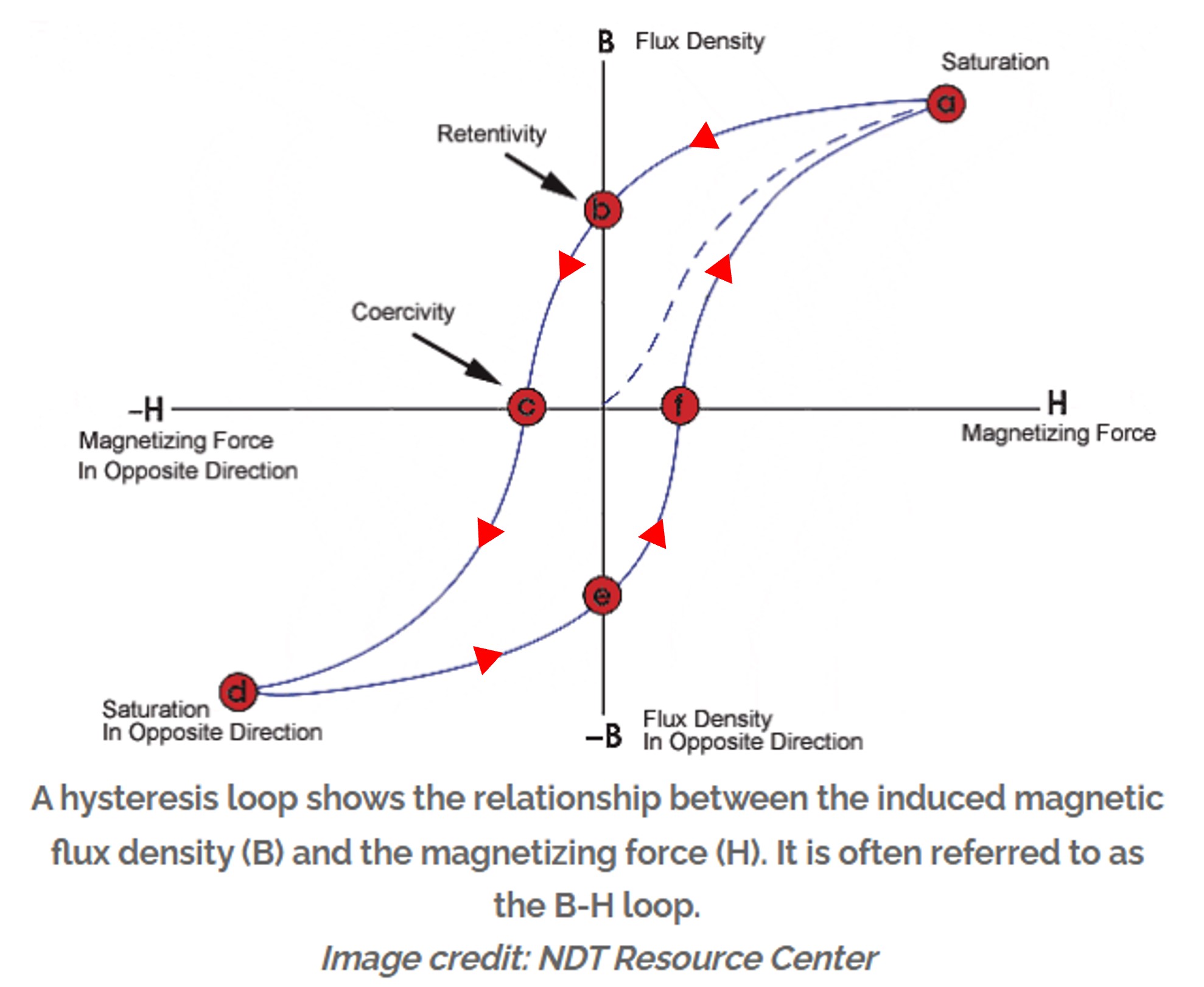
Hysteresis
Hysteresis loss is caused by the magnetization and demagnetization of the core as current flows in the forward and reverse directions. As the magnetizing force (current) increases, the magnetic flux increases. But when the magnetizing force (current) is decreased, the magnetic flux doesn’t decrease at the same rate, but less gradually. Therefore, when the magnetizing force reaches zero, the flux density still has a positive value. In order for the flux density to reach zero, the magnetizing force must be applied in the negative direction.
\(P_{b}\) = hysteresis loss (W)
η = Steinmetz hysteresis coefficient, depending on material (J/m3)
\(B_{MAX}\) = maximum flux density (Wb/m2)
n = Steinmetz exponent, ranges from 1.5 to 2.5, depending on material
f = frequency of magnetic reversals per second (Hz)
V = volume of magnetic material (m3)
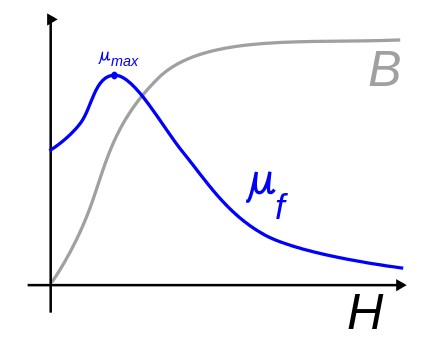
Side Effects - Saturation
If the current through a magnetic core coil is high enough that the core saturates, the inductance will fall and current will rise dramatically. This is a nonlinear threshold phenomenon and results in distortion of the signal. To prevent this, in linear circuits the current through iron core inductors must be limited below the saturation level.
Various Types of Inductors
Basic Electronics - Types of Inductors
Calculation of inductance
Series
Leq = L1 + L2 + … + Ln
Parallel
1/Leq = 1/L1 + 1/L2 + … + 1/Ln
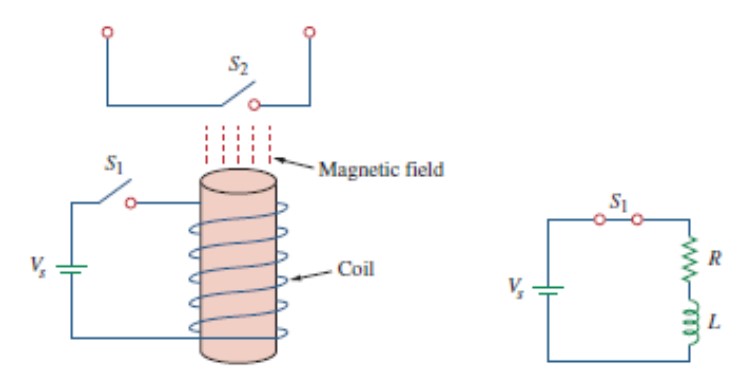
Applications
Relay Circuit

References
- Charles Alexander, Matthew Sadiku - Fundamentals of Electric Circuits-McGraw-Hill Science_Engineering_Math (2012)
- Thomas L. Floyd, David M. Buchla - Principles of Electric Circuits 10th ed
- DANIELLE COLLINS - Hysteresis loss and eddy current loss: What’s the difference?