Introduction
In electronics, unwanted noise always exists. To avoid misoperation, noises must be attenuated by filters. In real world, RC filter is commonly used for reducing high-frequency noises. Let’s look around various filter types.
Terminology
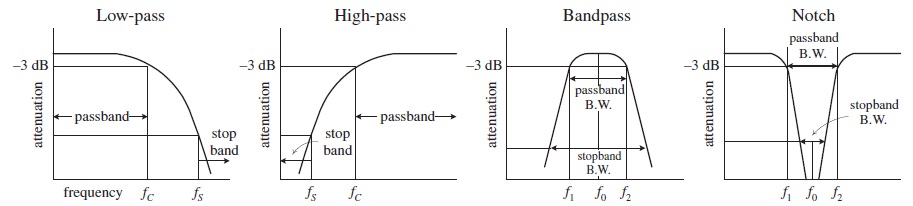
-3dB Frequency (\(f_{3dB}\))
This represents the input frequency that causes the output signal to drop to −3 dB relative to the input signal. The -3 dB frequency is equivalent to the cutoff frequency—the point where the input-to-output power is reduced by 1/2 or the point where the input-to-output voltage is reduced by 1/2. For low-pass and high-pass filters, there is only one -3 dB frequency. However, for bandpass and notch filters, there are two 3dB frequencies, typically referred to as \(f_{1}\) and \(f_{2}\).
Center frequency (\(f_{0}\))
On a linear-log graph, bandpass filters are geometrically symmetrical around the filter’s resonant frequency or center frequency—provided the response is plotted on linear-log graph paper (the logarithmic axis representing the frequency). On linear-log paper, the central frequency is related to the 3dB frequencies by the following expression:
\[f_{0} = \sqrt[2]{f_{1}f_{2}}\]For narrow-band bandpass filters, where the ratio of \(f_{2}\) to \(f_{1}\) is less than 1.1, the response shape approaches arithmetic symmetry. In this case, we can approximate \(f_{0}\) by taking the average of −3dB frequencies:
\[f_{0} = { {f_{1}+f_{2}} \over {2} }\]Passband
This represents those frequency signals that reach the output with no more than −3 dB worth of attenuation.
Stop-band frequency (\(f_{s}\))
This is a specific frequency where the attenuation reaches a specified value set by the designer. For low-pass and high-pass filters, the frequencies beyond the stop-band frequency are referred to as the stop band. For bandpass and notch filters, there are two stop-band frequencies, and the frequencies between the stop bands are also collectively called the stop band.
Quality factor (Q)
This represents the ratio of the center frequency of a bandpass filter to the −3 dB bandwidth (distance between −3 dB points \(f_{1}\) and \(f_{2}\)):
\[Q = { f_{0} \over {f_{2}-f_{1}} }\]For a notch filter, use \(Q = {f_{2}-f_{1}} \over f_{0}\), where \(f_{0}\) is often referred to as the null frequency.
Types
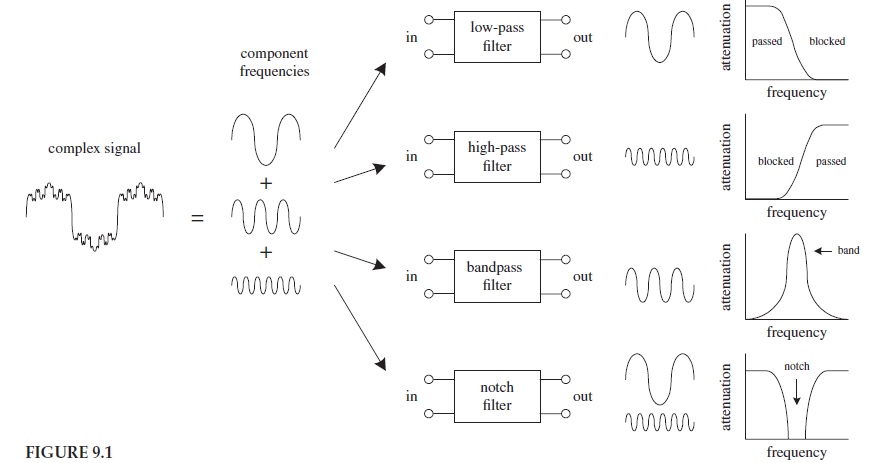
Filter type is determinded according to the purpose.
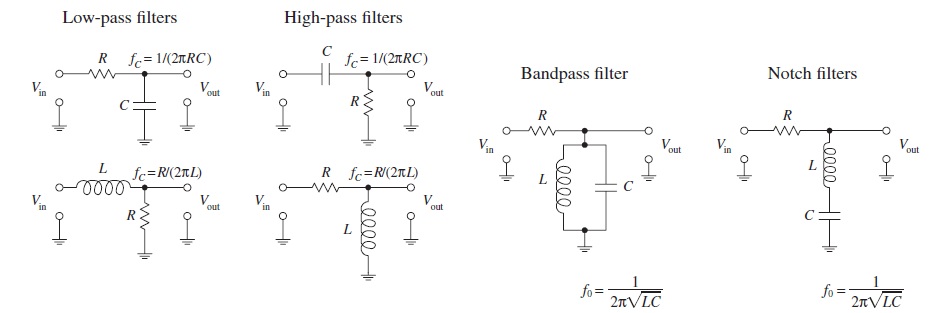
Basic filter circuits are as follows.

References
- Paul Scherz, Simon Monk - Practical Electronics for Inventors, 4th Edition